在公职类考试中,行程问题一直是考生谈之色变的一种题型。在具体考试中有很多题目也看似比较麻烦,但其实掌握该类题目的题型特征和做题方法就会有云开雾散的感觉。故今天就跟大家来分享一下考试中行程问题里的一个重要模型--牛吃草问题。
一、题型特征
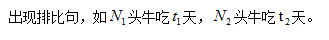
二、解题方法
牛吃草问题转化为相遇或追及模型来考虑。
三、常见考法
(一)标准牛吃草问题
同一草场问题是在同一个草场上的不同牛数的几种不同吃法,其中草的总量、每头牛每天吃草量“1”和草每天的生长数量,三个量是不变的。这种题型相对较为简单,直接套用牛吃草问题公式即可进行解答。
1.追及:一个量使原有草量变大,一个量使原有草量变小
原有草量=(牛吃草的速度-草生长的速度)×时间
例1.一片草场上草每天都均匀地生长,如果放24头牛,则6天吃完牧草;如果放21头牛,则 8天吃完牧草。问如果放16头牛,几天可以吃完牧草?
A.12 B.14 C.16 D.18
【答案】D。
【解析】题干描述中出现排比句且牛在吃草,草在匀速生长,所以是牛吃草问题中的追及问题,原有草量=(牛吃草的速度-草生长的速度)×时间,设每头牛每天吃1份草,草每天生长x份,16头牛t天可以吃完,根据原有草量相同,则有(24-x)×6=(21-x)×8=(16-x)×t,解得 x=12,t=18,即16头牛18天可以吃完牧草。故选D。
2.相遇:两个量都使原有草量变小
原有草量=(牛吃草的速度+草减少的速度)×时间
例2.由于天气逐渐冷起来,牧场上的草不仅不长大,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
【答案】5。
【解析】牛在吃草,草在匀速减少,所以是牛吃草问题中的相遇问题,原有草量=(牛吃草的速度+草减少的速度)×时间,设每头牛每天吃1份草,草每天减少x份,N头牛10天可以吃完,根据原有草量相同,则有(20+x)×5=(15+x)×6=(N+x)×10可解N=5。故可供5头牛吃10天。
(二)变型:极值型牛吃草问题
特征:最多能放多少头牛吃,草永远吃不完?
当让每天吃掉的草量小于等于每天生长的草量时,草永远都吃不完,故牛最多的头数与每天生长的草量相等时草永远吃不完。
例3.某河段中的沉积河沙可供80人连续开采6个月或60人连续开采10个月。如果要保证该河段河沙不被开采枯竭,问最多可供多少人进行连续不间断的开采?(假定该河段河沙沉积的速度相对稳定)
A.25 B.30 C.35 D.40
【答案】B。
【解析】题中出现“要保证该河段河沙不被开采枯竭,问最多可供多少人进行连续不间断的开采”属于极值型牛吃草问题。假设每个人每个月开采量为1,河沙每月沉积量为x,可列方程(80-x)×6=(60-x)×10,解得x=30。则每月开采量不能大过河沙沉积量,最多30人连续不断开采不会导致资源枯竭。故选B。
相信通过上面的详细讲解,大家一定能够很好地掌握牛吃草问题的各种类型,但是在考试时一般不会直接考大家,而是会把背景换成抽水问题、检票问题、资源开发等问题进行考察,这就需要大家能够很好地判断题型特征,将不同问题抽象为牛吃草问题并进行解答。










